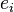 de una base vectorial inmersa en un espacio Euclídeo de dimensión n. Toda matriz representa una aplicación lineal entre dos espacios vectoriales de dimensión finita. La matriz identidad se llama así porque representa a la aplicación identidad que va de un espacio vectorial de dimensión finita a sí mismo.
de una base vectorial inmersa en un espacio Euclídeo de dimensión n. Toda matriz representa una aplicación lineal entre dos espacios vectoriales de dimensión finita. La matriz identidad se llama así porque representa a la aplicación identidad que va de un espacio vectorial de dimensión finita a sí mismo.Definición
Como el producto de matrices sólo tiene sentido si sus dimensiones son compatibles, existen infinitas matrices identidad dependiendo de las dimensiones. 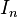 , la matriz identidad de tamaño
, la matriz identidad de tamaño  , se define como la matriz dia
, se define como la matriz dia
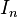 , la matriz identidad de tamaño
, la matriz identidad de tamaño  , se define como la matriz dia
, se define como la matriz dia
No hay comentarios.:
Publicar un comentario